上次写的微信版机器人的爬虫已经失效了,这次重新搞了爬虫,平常用的qq比较多所以也换成了qq版。
需要准备:
- Windows服务器一台,阿里云ECS即可(Linux也可以但是需要Wine,不如直接原生Windows)
- QQ小号一个,用来作为发送消息的载体
首先到coolq的社区下载最新版的coolq air,图灵版或者小i版都行,无所谓,我们不会用到他们的ai。
继续阅读“[娱乐] 一个监控NIKE官网NBA球衣打折的QQ机器人”
上次写的微信版机器人的爬虫已经失效了,这次重新搞了爬虫,平常用的qq比较多所以也换成了qq版。
需要准备:
首先到coolq的社区下载最新版的coolq air,图灵版或者小i版都行,无所谓,我们不会用到他们的ai。
继续阅读“[娱乐] 一个监控NIKE官网NBA球衣打折的QQ机器人”
复习一下我的数学知识T_T
回想高等数学中常见的多元数量函数$f:\mathbb{R}^{n}\rightarrow \mathbb{R}^{1}$,我们可以把他的输入当作一个向量 $\bf{x}\in \mathbb{R}^{n}$,输出$y=f(\bf{x})\in \mathbb{R}^{1}$是一个数字。那么由高数的知识我们知道$f$的梯度定义为
$$
\nabla f_{\boldsymbol{x}} \overset{\underset{\mathrm{def}}{}}{=} \left[ \frac{\partial f }{\partial x_1}, \frac{\partial f }{\partial x_2},\cdots,\frac{\partial f }{\partial x_n} \right]=\frac{\partial f }{\partial \boldsymbol{x}}
$$
有了上式,我们还可以写出全微分的向量化表示
\[接下来我们将其推广到向量函数。向量函数的“梯度”其实就是雅可比矩阵。
继续阅读“[数学] 向量函数的雅可比矩阵与链式法则”
观摩了微软俱乐部游戏组大佬的一个unity+tensorflow搞出来的的游戏AI之后对强化学习产生了点兴趣(其实说起来我当时进俱乐部面试的是游戏组最后给我整到软件了???),准备从小白开始学习一下强化学习和游戏里的AI。不过,查了很多资料之后直观感受是,国内这方面的优质资源真的很少,尤其是面向新手的。。。讲的乱七八糟,看的头皮发麻。经过一番扒拉后,找到了两个非常nice的国外大神做的入门教程,链接分别在
当我看到这两个Tutorial的时候感觉就像这位朋友的评论一样hhh

这里的代码用到的环境是openAI-gym里的Taxi-v2,这个游戏的界面长这样

简单说下这个图的含义:
总共5*5个空格,RGBY是四个表示乘客/目的地的位置 继续阅读“强化学习入门: Q-Learning的python实现”
写这个是因为今天在推CNN的反向传播的时候遇到了数学上无法理解的操作2333,google了一波发现主要问题出在我并没有学会矩阵求导运算,这个东西和普通的标量函数运算还是有很大区别的,比如认为AX对X的导数为A就是错的。因此今天专门来学习一下这个知识。
符号规定:使用小写字母x表示标量,粗体小写字母\[\boldsymbol{x} \]表示列向量,大写字母X表示矩阵。
首先思考一下标量函数对矩阵(向量)求导的定义,假设函数为f,求其对矩阵X的导数,可以记为
$$\frac{\partial f}{\partial X} = \left[\frac{\partial f }{\partial X_{ij}}\right]$$
可以发现我们要得到的其实是一个标量函数对矩阵X里的所有元素逐个求导然后把这些求导的结果根据与X里元素的位置关系排成与X同样形状的矩阵这么一个东西。当然我们可以把矩阵squeeze一下搞成一堆分离的变量逐个求,但是这样就与使用矩阵的初衷相抵触了,本来使用矩阵就是为了运算的方便整洁,那要拆开变成分散的变量还用矩阵干什么,所以有必要研究下从矩阵这个整体的角度出发的求导方法。
回想一下高等数学中多元函数的微分,可以写成
$$df = \sum_{i=1}^n \frac{\partial f}{\partial x_i}dx_i $$
换个写法把求和转变成向量内积的形式的话就是
$$df = \frac{\partial f}{\partial \boldsymbol{x}}^T d\boldsymbol{x}$$
按照之前的定义,矩阵的导数可以写成
$$df = \sum_{i=1}^m \sum_{j=1}^n \frac{\partial f}{\partial X_{ij}}dX_{ij}$$
那么同样的仿照上一段用矩阵表示多元函数微分的方式,比如内积表示这个式子的话,可以写成
$$df = \text{tr}\left(\frac{\partial f}{\partial X}^T dX\right)$$
其中tr表示矩阵的迹(仿真对角线元素之和),满足对尺寸相同的矩阵A,B,\[\text{tr}(A^TB) = \sum_{i,j}A_{ij}B_{ij}\],即\[\text{tr}(A^TB)\]是矩阵A,B的内积。
然后来考察一下基本的运算规则。 继续阅读“机器学习中的数学 –标量函数对矩阵求导的方法”
讲道理90%的工作都是在做图像处理。。。。opencv各种操作。
一完工赶紧专心复习emmmm
大致步骤:
首先必要的库
import cv2 import numpy as np import matplotlib.pyplot as plt import pytesseract from PIL import Image import os from PyQt5 import QtCore, QtGui, QtWidgets, Qt from PyQt5.QtCore import * from PyQt5.QtWidgets import *
① 预处理(灰度,直方图均衡,滤波)
def stechCr(img):
dst = cv2.equalizeHist(img)
if debug:
cv2.imshow('dst',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()
return dst
gray = cv2.fastNlMeansDenoisingColored(img, None, 10, 3, 3, 3)
gray=cv2.cvtColor(gray,cv2.COLOR_BGR2GRAY)
img,gray=makepic(gray)
② 提取ROI,主要用opencv的findContours找到背景下最大的轮廓,也就是卡面本身。
继续阅读“python小项目——实现校园一卡通图片信息识别”
在尝试了各种操蛋的手机端python ide之后忽然意识到可以在服务器上装jupyter然后手机浏览器打开emmmm
当然电脑端也能用啦,只不过我这台小鸡性能太垃圾所以意义不大
主要参考https://bitmingw.com/2017/07/09/run-jupyter-notebook-server/
不过他的文章中有一点问题就是,设置可以远程访问的时候有一步设置
c.NotebookApp.ip = '*'
,但是其实有时候是不行的(我也不知道为什么),如果不行就改成
c.NotebookApp.ip = '0.0.0.0'
另外,这是我用来跑ss的小鸡所以没有https的操作,直接跳过(反正我也懒得弄
基本上的步骤就是
①在服务器上装jupyter(废话
②生成配置文件 命令:
jupyter notebook --generate-config
③生成密钥 ,见下图
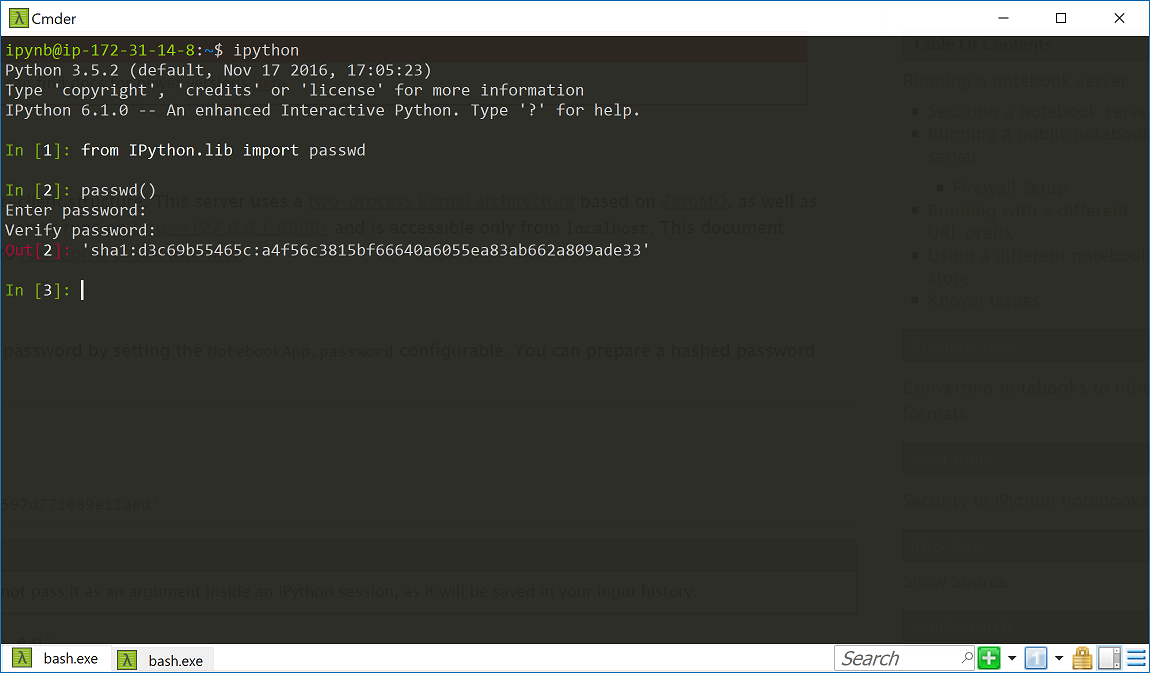
④修改配置文件
c.NotebookApp.ip='0.0.0.0' # 就是设置所有ip皆可访问 c.NotebookApp.password = u'sha:ce...' # 刚才复制的那个hash密钥 c.NotebookApp.open_browser = False # 禁止自动打开浏览器 c.NotebookApp.port =8888 #随便指定一个端口
⑤启动jupyter notebook应用,nohup 设置为断开ssh后继续运行的方式
# 启动 notebook 服务 nohup jupyter notebook > /dev/null 2>&1 &
如果想终止 notebook 应用,请找到含有 jupyter-notebook 的进程,并用 kill杀掉它。
⑥本地浏览器地址栏输入服务器ip:8888 就可以看到登录界面了,输入密码即可
